Applications
Tenseur des contraintes et tenseur des taux de déformation
Tenseur des contraintes
Dans un fluide visqueux, les forces de contact entre les éléments fluides comprennent à la fois les forces de pression et des cissions dues à la viscosité. Les cissions dépendent du taux de déformation des particules de fluide. On admet qu'elles résultent d'échange de quantité de mouvement à l'échelle moléculaire entre des particules ayant des vitesses différentes.
Le tenseur des contraintes \(\overline {\overline{\sigma}}\) peut se décomposer en la somme d'un tenseur sphérique \(\overline{\overline{\sigma}}_S\) et d'un tenseur déviateur \(\overline{\overline{\sigma}}_\delta\) de trace nulle.
\(\overline {\overline{\sigma}} = \overline {\overline{\sigma}}_S + \overline{\overline{\sigma}}_\delta\)
Tenseur des contraintes
Cette relation peut se noter :
Dans le cas du fluide parfait, σij = 0 et σii = -P, le tenseur des contraintes se réduit donc au premier terme.
Forces de contact
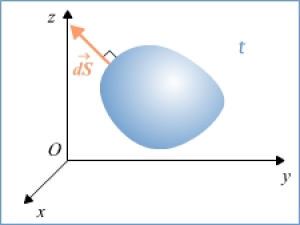
La résultante des forces de contact est :
Soit en utilisant le théorème de la divergence :
On obtient par unité de volume :
La résultante des forces de contact est égale à la divergence du tenseur des contraintes
Tenseur des taux de déformation
Ce tenseur a été introduit en cinématique
Dans cette expression, u, v, w sont les composantes de la vitesse dans un référentiel O, x, y, z
Remarque :
la trace de ce tenseur est égale à la divergence de la vitesse (div \(\overrightarrow{V}\))
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.