Applications
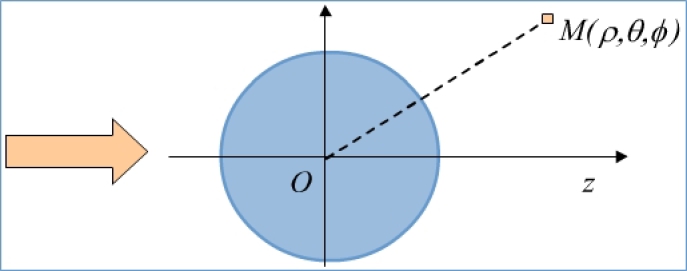
Écoulement visqueux incompressible autour d'une sphère immobile
Hypothèses : Écoulement permanent, fluide incompressible, on néglige les effets de la pesanteur sur l'écoulement.
\(\rho\) : masse volumique
\(\mu\) : viscosité dynamique
\(v\) : viscosité cinématique
\(\overrightarrow{V_0}\) : vitesse loin de l'obstacle
Nous procédons comme précédemment : écriture de l'équation de Navier Stokes :
Équation réduite
On utilise les variables réduites suivantes :
\(P' = \frac{P}{\rho V_0^2} ; z' = \frac{z}{a} ; r' = \frac{r}{a}\)
Les vitesses sont rapportées à V0.
L'équation réduite s'écrit donc sous forme vectorielle :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Détermination de la somme F des forces de frottement appliquées à la sphère
On considère la grandeur réduite associée à F suivante : \(\frac{F}{\rho V_0^2 a^2}\)
Ce qui donne comme condition de similitude :
L'étude expérimentale est simplifiée puisque le seul paramètre intervenant dans le problème est le nombre de Reynolds.