Applications
Notion de pertes de charge
Hypothèses
L'écoulement est permanent : \(\frac{\partial \overrightarrow{V}}{\partial t} = 0\)
Les forces de volume se réduisent à la pesanteur :\( \overrightarrow{F} = - \overrightarrow{grad} (\rho g z)\)
Le fluide est incompressible : \(\rho = cste \) et \(\mbox{div}\overrightarrow{V} = 0\)
Démonstration
Écrivons l'équation de Navier Stokes
\[\begin{array}{l}
\rho ({\frac{\partial \overrightarrow{V}}{\partial t}} + \frac{1}{2} \overrightarrow{grad} V^2 + \overrightarrow{rot} \overrightarrow{rot} \overrightarrow{V}) = - \overrightarrow{grad} (P + \rho g z) + \mu \Delta \overrightarrow{V} \\
=0\\
\mbox{mouvement permanent}\\
\mu \Delta \overrightarrow{V} - \overrightarrow{grad} (P + \rho g z + \rho \frac{V^2}{2}) = \rho - \overrightarrow{rot} \overrightarrow{V} \wedge \overrightarrow{V}
\end{array}\]
Prenons la circulation élémentaire sur une ligne de courant :
\[\begin{array}{l}
\overrightarrow{grad} (P+ \rho g z + \rho \frac{V^2}{2}). \overrightarrow{d l} = \mu \Delta \overrightarrow{V}.\overrightarrow{d l} \\
=d (P+ \rho g z + \rho \frac{V^2}{2}) = \mbox{ Variation de charge}
\end{array}\]
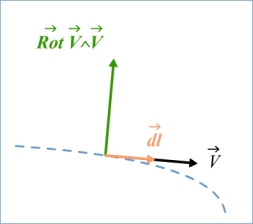
Ce résultat montre que la charge totale de l'écoulement n'est pas constante le long d'une ligne de courant.
\(\mu\) \(\Delta\) \(\overrightarrow{V}\).\(\overrightarrow{d l}\) ce terme représente la perte de charge linéaire le long de la ligne de courant en J.m-3